Interactive Grain
Image Segmentation
using Graph Cut Algorithms
Jarrell Waggoner$^1$ / @malloc47 / waggonej@email.sc.edu,
Youjie Zhou$^1$,
Jeff Simmons$^2$,
Ayman Salem$^3$,
Marc De Graef$^4$,
Song Wang$^1$
$^1$USC, $^2$AFOSR, $^3$MRi, $^4$CMU
Interactive Segmentation?
- Contrast with fully-automatic segmentation
- Sparse number of user interactions as additional constraints or guidance in the segmentation process
- Other interactive segmentation methods use:
- Bounding boxes
- Coarse outlining of the desired boundary
- "Scribbling" foreground/background regions
Our Approach
- Build on our previous propagation method
- Correct errors after every propagation with a single point (click) as the user-supplied interaction
- Reduce having to draw individual boundaries
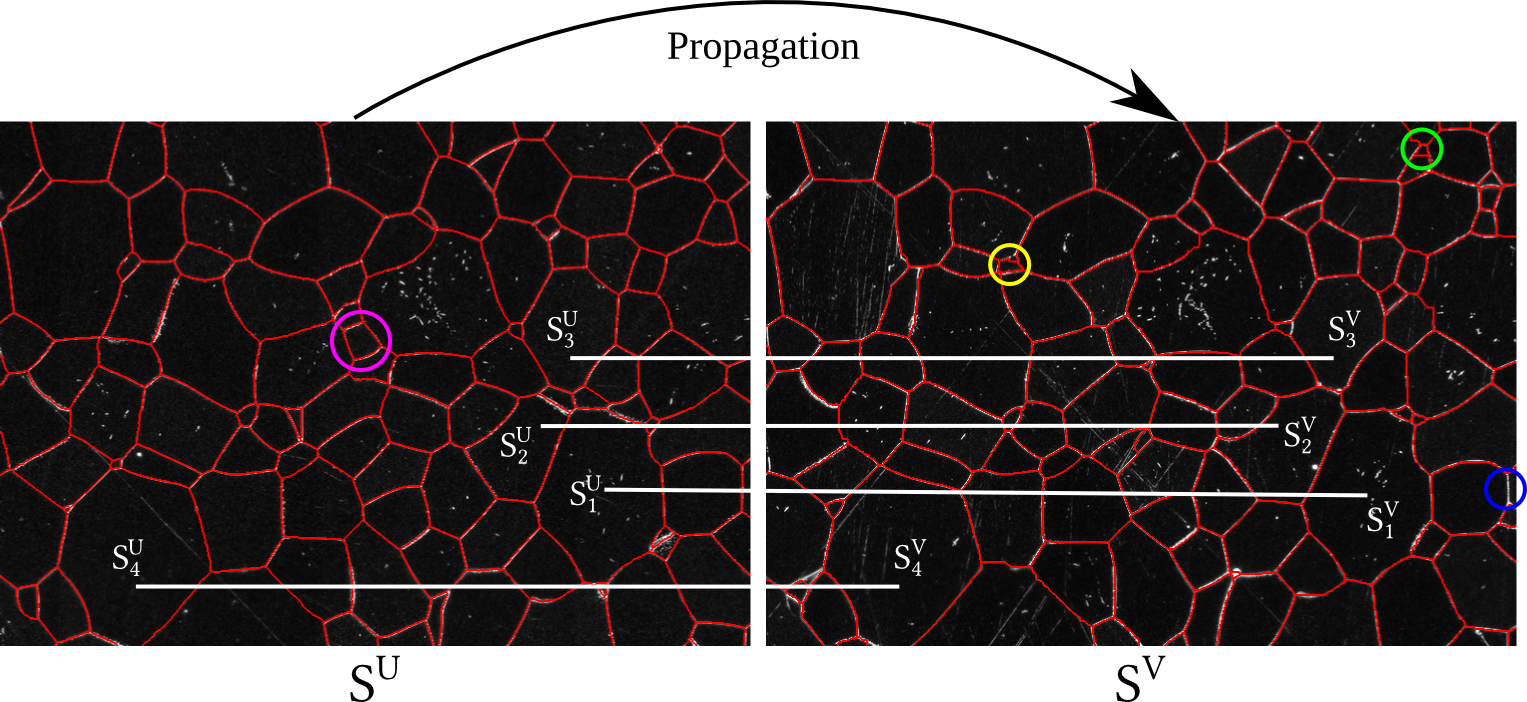
| $U$ | : Source image that is segmented |
| $V$ | : Target image that is not segmented |
| $S^U, S^V$ | : Segmentation of $U$ or $V$ respectivesly |
Propagation
- Obtain $S^V$ by propagating $S^U$ to $V$
In our previous work, this was done by using an energy of the form
\begin{equation} E( S^V ) = \sum_{p\in V}\Theta_p(S^V_i) + \sum_{\{p,q\}\in\mathcal{P}^V_n} \Phi_{pq}(S_i^V , S_j^V) \end{equation}which can be minimized by the min-cut max-flow graph cut algorithm
Unary and Binary Terms
\begin{equation} \Theta_p(S^{V}_i) = \left\{ \begin{array}{lcr} 0, & \textrm{distance}(p,S^U_i) < d \\ \infty, & \textrm{ otherwise} \\ \end{array} \right. \end{equation}
\begin{equation} \Phi_{pq}(S^V_i , S^V_j) = \left\{ \begin{array}{lcr} 0, & i = j \\ \infty, & \{ S^U_i, S^U_j \} \notin \mathcal{A}^U \\ g( p, q ), & \{ S^U_i, S^U_j \} \in \mathcal{A}^U \\ \end{array} \right. , \end{equation}
Limitations
- Minimizes a fixed set of segments: must use heuristics to determine where to add new segments
- Topology constraints may not allow the removal of some segments
Goal:
Incorporate human interaction into the segmentation task to
- Remove Spurious Segments
- Add Missing Segments
Do this with minimal interaction, producing an updated segmentation $\tilde{S}^V_i$
Removal
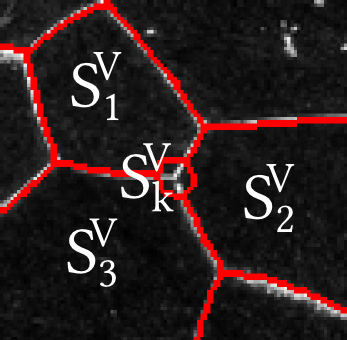
Removal Input
We require only a single annotation (click) identifying a particular segment $S^V_k$ to be removed, which is done in two steps:
Identify Local Region
Identify local region for removal $\mathcal{L} = \{\mathcal{A}^V\}_k \bigcup S^V_k$ where $\{\mathcal{A}^V\}_k$ is all the segments adjacent to the segment to be removed
Update Energy Terms
Update the unary term to allow $S^V_k$ to be
reassigned to its neighbors:
\begin{equation}
\begin{aligned}
\forall p \in S^V_k ,& \quad \Theta_p(\tilde{S}^V_i) = \left\{
\begin{array}{lcr}
0, & S^V_i \in \{\mathcal{A}^V\}_k \\
\infty, & \textrm{ otherwise} \\
\end{array}
\right. \\
\forall p \notin S^V_k ,& \quad \Theta_p(\tilde{S}^V_i) = \Theta_p(S^V_i)
\end{aligned}
\end{equation}
Removal Algorithm

Addition
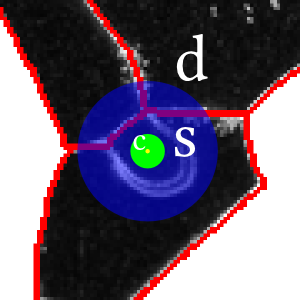
Addition Input
Require three inputs:
- Center point $c$ for new segment
- Seed radius $s$ around the center point which is completely contained within the desired grain
- Dilation radius $d$ around the center point which completely covers the desired grain
Local Region
$\mathcal{L} \gets$ union of all segments that contain a seed pixel or dilation pixel
Update Energy Terms
\begin{equation} \Theta_p(\tilde{S}^V_{n+1}) = \left\{ \begin{array}{lcr} 0, & \| p - c \| \leq d \\ \infty, & \textrm{ otherwise} \\ \end{array} \right. \end{equation} \begin{equation} \Theta_p(\tilde{S}^V_i) = \left\{ \begin{array}{lcr} \infty, & \| p - c \| \leq s \textrm{ and } i \neq n+1 \\ \Theta_p(S^{V}_i), & \textrm{ otherwise.} \\ \end{array} \right. \end{equation}
Addition Algorithm

Parameter
Estimation
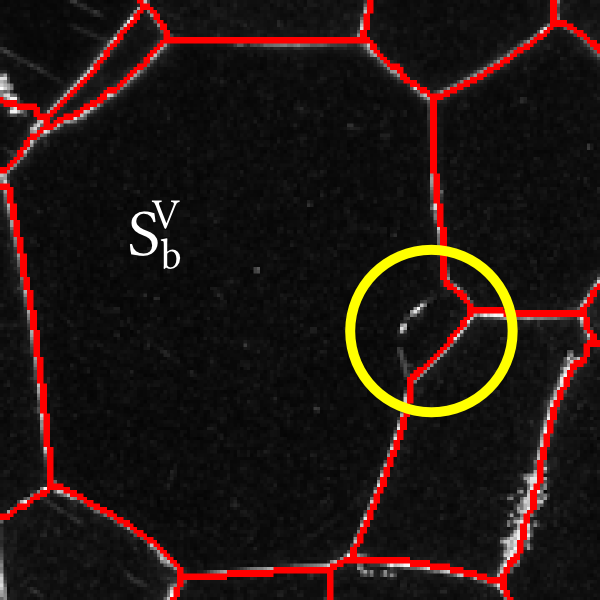
Parameter Estimation
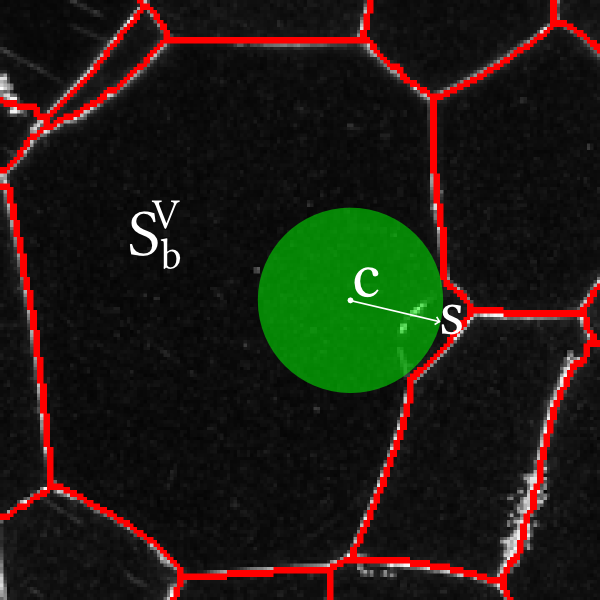
- Estimate the $s$ and $d$ parameters in the addition step
- Do this by leveraging information about the center $c$
the user provided relative to the initial segment in which
it resides:
- Increase $s$ by $\epsilon$ until it touches the boundary of its containing segment $S^V_b$
- Set $d$ to be $2\times s$
Parameter Estimation Visual Example


Experiments
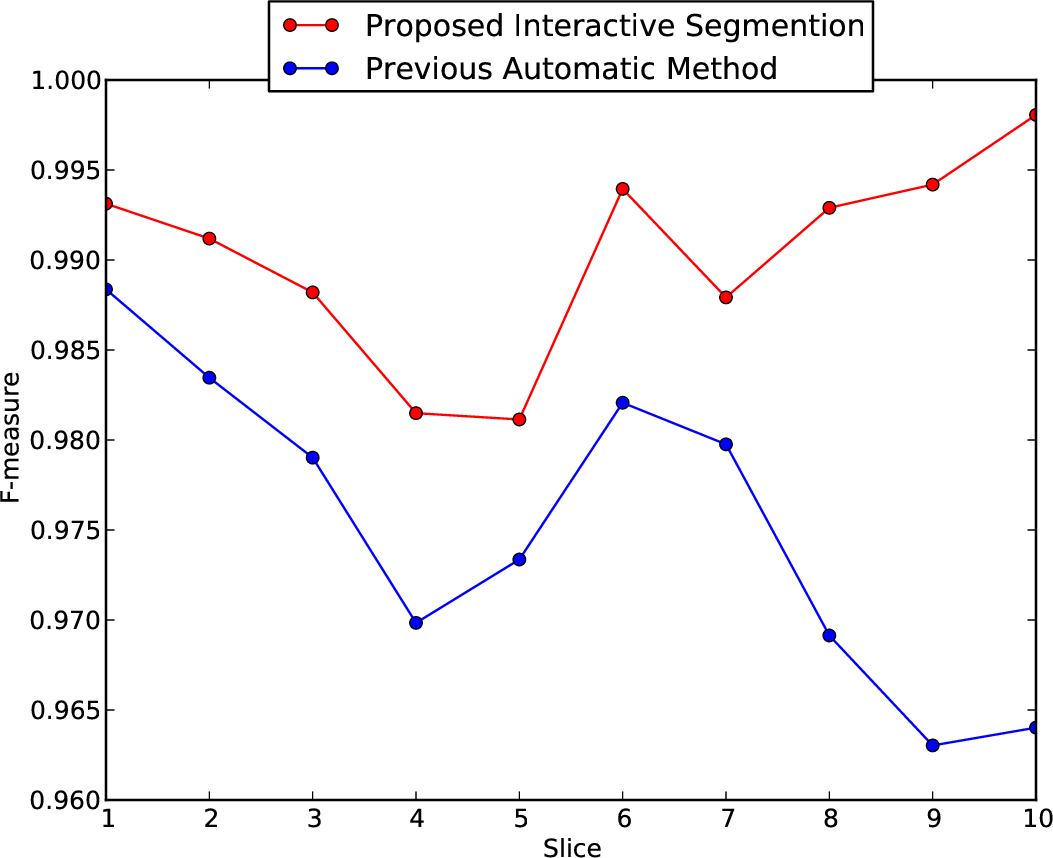
Performance
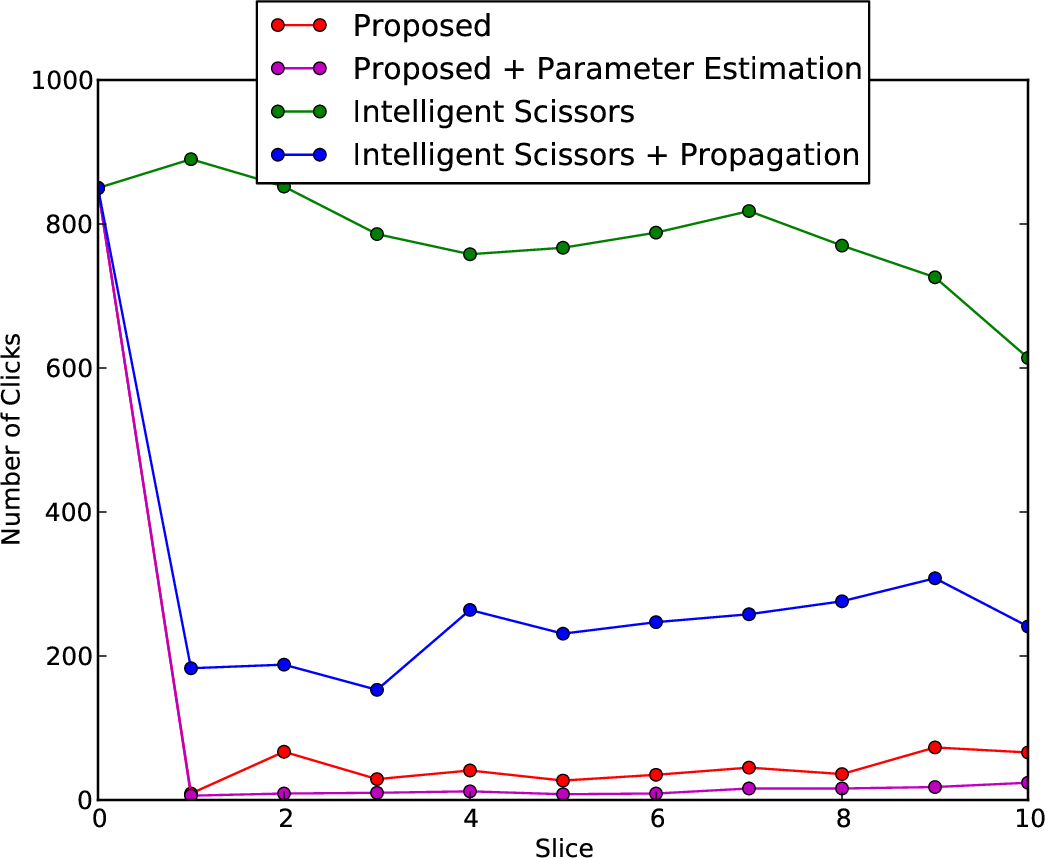
Effort
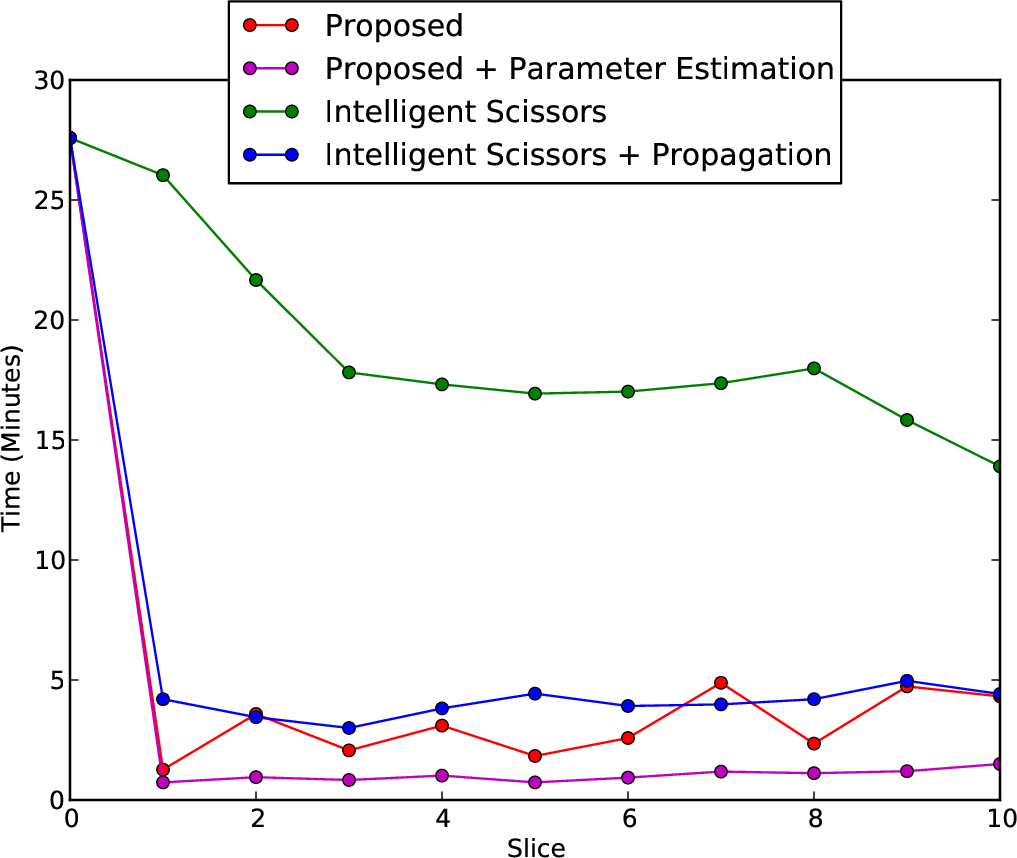
Time
Qualitative Results
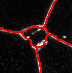
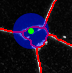
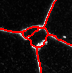

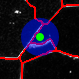







Conclusion
- Augmented our previous propagation approach with an interactive component that increases performance
- We handle both segmentation addition and removal using minimal interaction
- Parameter estimation reduces the time and effort needed